Immagina di trovarti in una festa con almeno sei persone scelte totalmente a caso. Quante sono le persone che si conoscono tra di loro o che non si conoscono tra di loro?
A questa domanda è possibile rispondere indicando un numero ben preciso. Infatti, il Teorema degli amici e degli sconosciuti
afferma che in ogni festa di sei persone, almeno tre di esse sono reciprocamente sconosciute oppure almento tre di esse sono reciprocamente amiche.
Questo teorema è un caso particolare della Teoria di Ramsey, che è un ramo della matematica che si occupa di stabilire qual
è il minor numero di elementi necessario affinché una certa proprietà sia vera. Quindi, nel caso degli amici e degli sconosciuti, il numero di elementi
indica il numero di persone, mentre la proprietà da soddisfare è che "almeno tre si conoscono a vicenda oppure almeno tre non si conoscono tra di loro".
Dimostrazione per casi
Il teorema può essere facilmente dimostrato esaminando tutti i possibili casi.
Si inizia creando un grafo completo, in cui ogni nodo rappresenta una persona presente alla festa e è collegato con tutti gli altri nodi.

Figura 1. Ogni nodo rappresenta una persona. Ogni nodo viene collegato con tutti gli altri.
A questo punto si scelgono due colori (ad esempio rosso e blu) e si colorano i nodi e gli archi a seconda del rapporto (amici o sconosciuti) tra le due persone e si calcolano tutti i possibili casi

Figura 2. Le 76 possibili combinazioni amici-sconosciuti in un grafo di 6 nodi. In qualsiasi grafo, esiste sempre una tripletta di nodi rossi o blu che sono reciprocamente amici o sconosciuti.
Dimostrazione alternativa
Una dimostrazione alternativa si basa sul principio dei cassetti. Il principio dei cassetti afferma che se si hanno n cassetti
e n+k oggetti (con k maggiore di zero), allora almeno un cassetto deve contenere più di un oggetto. Immagina di avere dieci cassetti e undici anelli e di
voler mettere gli anelli nei casetti: dove metti l'undicesimo anello? Bisogna per forza avere un cassetto con due anelli.
Uno volta chiarito tale principio, si può iniziare con la dimostrazione.
Innanzitutto si sceglie un vertice a caso, indicandolo con P. Siccome
il grafo ha 6 nodi ed è completo, ci saranno cinque archi collegati a P (vedi Figura 1).
Ognuno di questi cinque archi sarà di colore rosso oppure blu; il principio
dei cassetti afferma che almeno tre di essi devono avere lo stesso colore
(immagina di avere un cassetto blu, uno rosso e cinque anelli: ci sarà sicuramente un cassetto con almeno tre anelli.).
Indichiamo i tre nodi collegati a P tramite archi dello stesso colore (ad esempio blu) con A, B, C.
Ad esempio:
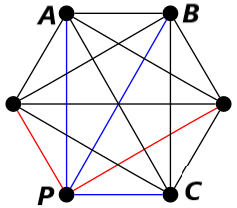
Figura 3. Siccome il grafo è completo, scegliendo un nodo P a caso, tale nodo avrà sempre cinque archi. Per il principio dei cassetti, almeno tre di questi archi hanno lo stesso colore.
Ora si può notare che per qualsiasi tripletta di nodi A, B, C tali nodi formeranno sempre un triangolo (perché il grafo è completo). Infatti nel caso della Figura precedente:

A, B, C formano il triangolo evidenziato in verde.
Ora possono succedere due cose: nessuno degli archi che formano il triangolo è blu, quindi tutti gli archi sono rossi, formando appunto un triangolo rosso (la proprietà del teorema è soddisfatta). Oppure, se uno degli archi che formano il triangolo è blu (ad esempio l'arco che colleda B ad A), allora si forma un triangolo blu con P (soddisfando la proprietà del teorema).
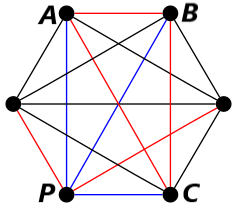

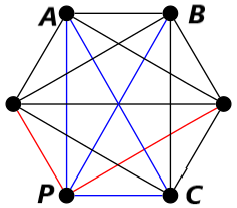
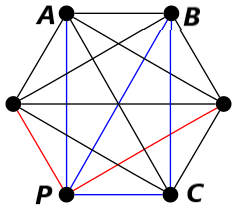
Da sinistra verso destra sono presenti quattro possibili casi: nessun arco del triangolo è blu, quindi si forma un triangolo rosso. L'arco AB è blu, creando così il triangolo blu ABP. L'arco AC è blu, formando il triangolo blu ACP. L'arco BC è blu, generando il triangolo blu BCP.
